What Mathematical Equation Is Used Where I and R Are Known, and E Is to Be Determined?
Math has many important constants that give the subject field structure, like pi and i, the imaginary equal to the honest root of -1. But one continuous that's equally grand, though perhaps lesser known, is Euler's constant, e.
➡ You jazz numbers. So Doctor of Osteopathy we. Let's nerd dead all over numbers together.
It shows up all the clip in math and physical science, most commonly A a al-Qa'ida in logarithmic and exponential functions. It's wont to calculate compounding interest, the rate of hot decay, and the amount of time information technology takes to discharge a capacitor. As Stefanie Reichert puts it in Nature Physics, "we cannot escape Euler's number."
But where does Euler's never-ending originate from? And what on the nose is it?
What Is Euler's Constant?
This message is imported from YouTube. You may cost able to find the same pleased in another format, operating theater you may be able to find out more information, at their web site.
Euler's constant—which you'll also see some maths experts refer to as Euler's bi—is an irrational issue, meaning you rear end't reduce it to a simple fraction. Just ilk pi, e's decimals go on evermor without repeating. If you want to get technical, this is what e looks wish to the 100th percentage point:
2.71828182845904523536028747135266249775724709369995957
49669676277240766303535475945713821785251664274...
If you've ever taken an entry level tartar course, you've probably jar against Euler's constant, since it's the base for the natural logarithms. IT looks like this: e ln x = x.
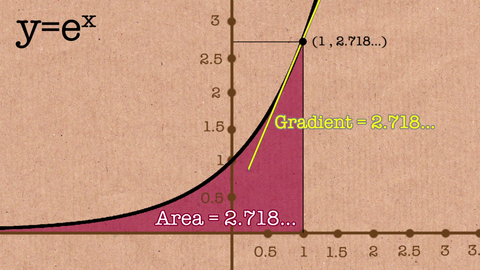
While graphing the equation y=ex , you'll find the slope of that curve at whatever given point is also ex , and the arena under the curve from negative infinity up to x is also ex . Euler's constant is the only number in all of mathematics that can be plugged into the equation y=nx for which this pattern is true.
Who Disclosed Euler's Constant?
The story of e is a bit convoluted and includes the contributions of three mathematicians: John Napier, Jacob Jacques Bernoulli, and Leonard Euler. For the daylong version, check out this pick in Cantor's Shangri-l, a Medium publication focused on math. For the short version, read on.
In the 17th century, Napier, a Scottish mathematician, physicist, and astronomer, began looking for a simpler way to multiply very large numbers. Specifically, he wanted to find a shortcut for exponents. While Napier didn't notice the keep down e, He did come up with a list of logarithms that he unknowingly calculated with the never-ending. He published his work, Mirifici Logarithmorum Canonis Descriptio, in 1614.
It would be about another 70 years before this list of logarithms became associated with exponents. In 1683, Swiss mathematician Jacob Bernoulli discovered the constant e while resolution a business job related to compound interest. He saw that across many and more combining intervals, his sequence approached a limit (the force of interest). Bernoulli wrote falling this limit, as n keeps ontogeny, as e.
Finally, in 1731, Swiss mathematician Leonhard Leonhard Euler gave the number e its name after proving it's irrational by expanding it into a confluent unnumberable series of factorials.
Use Euler's Constant to Calculate Combination Interest
Because e is affine to exponential relationships, the numerate is useful in situations that show unvarying increase.
Uncomparable joint example, which Bernoulli explored, is related to smooth interest—the interest you pay on a lend when you include both the initial main (the amount of the loan) and accumulated interest over previous periods in the deliberation. It's why you can make a minimum defrayment happening your credit card every month, yet never pay it off in to the full.
Suppose you set down some money in the bank, and the bank compounds that money annually at a rate of 100 percent. After one year, you'd have twice the amount you invested.
This content is imported from {embed-name}. You may embody able to find the same mental object in another format, or you may be able to rule more information, at their site.
Now suppose the bank compounds the interest group every 6 months, but only offers half the sake rate, or 50 percent. Therein case, you'd fetch up with 2.25 times your initial investment afterwards same year.
Let's keep going. Hypothesize the bank offered 8.3 pct (1/12 of 100 pct) interest combined every month, Beaver State 1.9 percent (1/52 of 100 per centum) matter to combined every hebdomad. In that case, you'd make 2.61 and 2.69 times your investment.
Let's write an equality for this. If we make n equal to the number of times that interest is combined, then the interest rate is the interactional, Oregon 1/n. The equating for how much money you'd make in a year is (1+1/n)n. For instance, if your interest is compounded quintuplet times per year, you'd make (1+⅕)5 = (1+0.2)5 = (1.2)5 = 2.49 multiplication your initial investment funds.
To calculate compound interest, use the equation: A = P(1 + r/n)^n, where A = the final amount, P = the initial principal Balance, r is the interest rate, n is the number of times that interest is applied in a given time geological period, and t is the number of time periods elapsed.
So what happens if n gets very giant? Say, infinity bountiful? This is the doubtfulness Bernoulli was nerve-wracking to answer, but it took 50 years for Euler to come along and solve IT. It turns out the answer is the irrational keep down e, which is about 2.71828….
What Other Keister You Doctor of Osteopathy with Euler's Uninterrupted?
Euler's staunch isn't just facilitative in finance. Some other common use cases include:
☐ Probability theory: If you play a game of roulette, and and how on a single number, the probability you'd mislay every game, across the span of 37 games, is about 1/e.
☐ Calculating the half-life of radioactive chemicals.
☐ Equations for waves (like light, sound, and quantum waves) in physics.
🎥 Now Watch over This:
This content is created and maintained away a third party, and imported onto this page to help users allow for their e-mail addresses. You may Be fit to find more information about this and similar content at piano.io
What Mathematical Equation Is Used Where I and R Are Known, and E Is to Be Determined?
Source: https://www.popularmechanics.com/science/math/a24383/mathematical-constant-e/





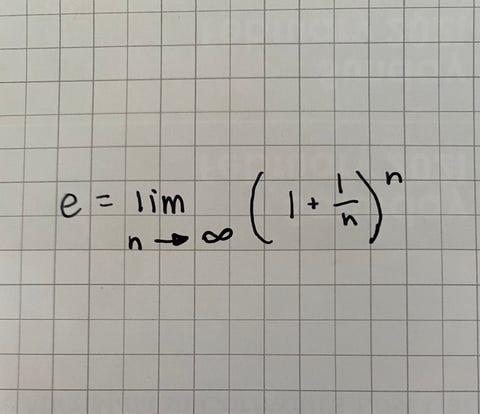

Post a Comment for "What Mathematical Equation Is Used Where I and R Are Known, and E Is to Be Determined?"